And here's to number x in my brief foray into women and the sciences...Maria de Agnesi

 She was one of the earliest 'glitterati' of Calculus, right up there with Sir Isaac Newton.  She was one of the first to write an important text in the subject, and was even more notable, in my humble opinion, because she was a woman of the eighteenth century.

ok, so she is not exactly Hedy Lamarr, but who cares?

"Her innovation was an equation known as "the witch of Agnesi."  Now, I cannot add two and two (which clearly equals 2,234), so I am going to quote from a better source than my mathematically challenged brain:

The "witch of Agnesi" is a curve studied by Maria Agnesi in 1748 in her book Instituzioni analitiche ad uso della gioventù italiana (the first surviving mathematical work written by a woman). The curve is also known as cubique d'Agnesi or agnésienne, and had been studied earlier by Fermat and Guido Grandi in 1703.

The name "witch" derives from a mistranslation of the term averisera ("versed sine curve," from the Latin vertere, "to turn") in the original work as avversiera ("witch" or "wife of the devil") in an 1801 translation of the work by Cambridge Lucasian Professor of Mathematics John Colson (Gray).

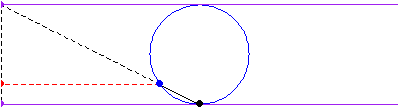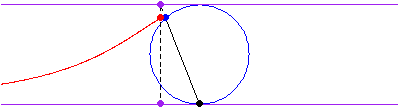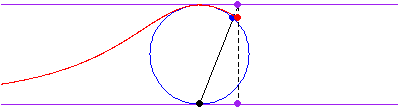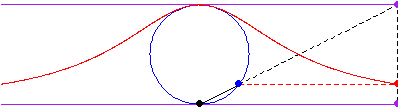
The curve is obtained by drawing a line  from the origin through the circle of radius  and center , then picking the point with the  coordinate of the intersection with the circle and the  coordinate of the intersection of the extension of line  with the line .

In parametric form,

			(1)
			(2)

for , or

			(3)
		(end quote)

https://mathworld.wolfram.com/WitchofAgnesi.html  

Now, please don't ask me what the hell those numbers mean.  I include this language, for those of you who do comprehend the beauties of abstract mathematical equations.  While my brain isn't comfortable in this realm, I can yet appreciate the symmetry of certain concepts.

Unfortunately for me, in my research, it has been difficult to isolate a concise explanation of what this woman's work accomplished for her field in the long term.  What, for example, were the practical applications of this work?

Well, first, the 'witch' appears to be important in probability theory.  Probability theory is defined as:

Probability theory is the study of uncertainty....  The mathematical theory of probability is very sophisticated, and delves into a branch of analysis known as measure theory. In these notes, we provide a basic treatment of probability that does not address these finer details. 1 Elements of probability In order to define a probability on a set we need a few basic elements, • Sample space Ω: The set of all the outcomes of a random experiment. Here, each outcome ω ∈ Ω can be thought of as a complete description of the state of the real world at the end of the experiment. • Set of events (or event space) F: A set whose elements A ∈ F (called events) are subsets of Ω (i.e., A ⊆ Ω is a collection of possible outcomes of an experiment).1 . • Probability measure: A function P : F → R that satisfies the following properties, - P(A) ≥ 0, for all A ∈ F - P(Ω) = 1 - If A1, A2, . . . are disjoint events (i.e., Ai ∩ Aj = ∅ whenever i 6= j), then P(∪iAi) = X i P(Ai) These three properties are called the Axioms of Probability. Example: Consider the event of tossing a six-sided die. The sample space is Ω = {1, 2, 3, 4, 5, 6}. We can define different event spaces on this sample space. For example, the simplest event space is the trivial event space F = {∅, Ω}. Another event space is the set of all subsets of Ω. For the first event space, the unique probability measure satisfying the requirements above is given by P(∅) = 0, P(Ω) = 1. For the second event space, one valid probability measure is to assign the probability of each set in the event space to be i 6 where i is the number of elements of that set; for example, P({1, 2, 3, 4}) = 4 6 and P({1, 2, 3}) = 3 6 . Properties: - If A ⊆ B =⇒ P(A) ≤ P(B). - P(A ∩ B) ≤ min(P(A), P(B)). - (Union Bound) P(A ∪ B) ≤ P(A) + P(B). - P(Ω \ A) = 1 − P(A). - (Law of Total Probability) If A1, . . . , Ak are a set of disjoint events such that ∪ k i=1Ai = Ω, then Pk i=1 P(Ak)....

http://cs229.stanford.edu/section/cs229-prob.pdf

OK, I'm lost, but you might not be.  

Biography (or an area where I find myself a little more comfortable...

She was the child of Pietro de Agnesi--whose family made their considerable fortunes in silk.  Ole Pietro had three wives over the course of his life, and 21 children.  Twenty-one.  Ummmmmmmmm.  Enough said.

Her father doted on his children, but particularly on his daughter, on whom he bestowed a superior education in the form of tutors from the best universities.  Maria early on achieved a mastery of Latin, Greek and Hebrew.

It was in 1738, that de Agnesi published "Propositiones Philosophicae"--a series of essays about natural science (which in eighteenth century terms referred to a lovely combination of philosophy and experimental science, and mathematics).  She also presided over her father's salons;  which was a popular form of social gathering at the time, where intellectuals, artists, musicians, and other members of the liberal elite met and exchanged ideas.  I think that the salon (and other intimate social gatherings) would turn out to become one of the most powerful mechanisms for social change of the 18th century.  I think the modern day equivalent would be facebook.

de Agnesi, did not like such public gatherings however, and gradually withdrew from the public eye, preferring a life geared towards religious contemplation and private intellectual exploration.  She dressed more simply, and even briefly thought about entering a convent.  

Given the opportunity to further her studies in mathematics, de Agnesi was allowed by her father to study with one of the pre-eminent scholars of the age--Ramiro Rampinelli, who had been a professor at Milan, and briefly in Rome.  Rampinelli became a frequent visitor at her father's house, and over time furthered Maria' s exploration into calculus.  Later, she would write and successfully publish a text on differential calculus.

Differential calculus is a method which deals with the rate of change of one quantity with respect to another. 

https://byjus.com/maths/differential-calculus/#:~:text=What%20is%20differential%20calculus%3F,calculus%20concepts%20apart%20from%20integrals.

With the financial aid of her father, she was able to publish her book...and you can imagine how rare and difficult this would be.  The work (after many, many months), was eventually published as two volumes .  Her treatise was, in effect, a distillation of the work of top mathematicians in the European community, in addition to her own innovations.

Now, it gets really cool.

After her work became both famous and admired, she was even tapped by Pope Benedict XIV to become chair of mathematics at the University of Bologna.  Dude!

But, Maria had already retreated into the religious life, eventually even withdrawing within her father's household, by living in separate rooms, where she also devoted herself to the care of elderly women.  What a gal!  She never even visited Bologna.

Her father, who had dominated her life, finally died in 1752.  Thereafter, de Agnesi devoted herself entirely to good works, eventually spending her entire fortune on various charities.

She died, impoverished, at a poorhouse she had helped found.

  As with many people of achievement, Maria's end was somewhat tragic, as were the missed opportunities.  Clearly ahead of her time, one wonders what she could have accomplished, had she not been so enamored of the religious life.  Oops...I am showing bias.  Forgive me, Dear Reader.

And so, on to the next subject....