What do you know about quantum physics? Astrophysics? String theory? Anything?
Me neither. I know someone who is studying to be an astrophysicist. Impressive, right? Damn, I always wanted to skip around in the realm of higher mathematics and its' sister discipline quantum physics. Together, with the other physical sciences, its' language has created a chaste, beautiful space.
As for me, I only know one mathematical phrase: 2 + 2 = 1,546,345,987.
Now, we all know this guy:
Einstein's work didn't happen in a vacuum. As with other pivotal moments in the theoretical sciences, E=MC squared was part of a larger body of work, from a collection of pretty bitchin' physicists. This week, I want to tell you about a physicist and math dude who has been largely forgotten by non-scientifically (i.e. mathematically) inclined folks: Arthur Eddington.
I know, Dear Reader, I know: you've probably never heard of him, right? Me neither. But, hopefully, we live and learn. Sadly, Eddington's work is largely forgotten today by the mathematically challenged (like moi), but we all know about Einstein, don't we? Why is that? I don't know, maybe we liked Albert's hair, or his penchant for the ladies (didn't you know that Einstein couldn't keep his dick in his pants? Why is it that a lot of these celebrated scientists can't just stick to one woman? If you don't believe me, take a look at Robert Oppenheimer. I mean, is it the math thing? Hmmm. Maybe I have something there: math + notoriety = ladykiller?????????).
But let's take a look at the Eddington's life and work, yes?
Arthur was born on 12/28/1882, to Quaker parents (a fact I find really interesting: the religion espouses complete non-violence, yet Eddington's work, along with others, would inevitably lead to weapons of mass destruction --such as the bomb. This begs the question, could Eddington conceive of a logical end result to the larger work? Couldn't he conceive of where relativity theory would inevitably lead? Bueller? Bueller? I have always thought, perhaps in error, that 'science for sciences' sake was not an adequate argument--perhaps things would've been different if these guys remembered that you didn't always find treasure in the Emerald City).
Eddington's father died when he was 2, so his early education was left up to his single mother. From the beginning, I think it was clear Arthur had a talented mind, although the restrictions of primary school didn't always indicate the potential of a creative intellect. He was home-schooled for a time, but eventually ended up at Owens College (later known as the University of Manchester). He graduated with a degree in physics in 1902. Arthur won a scholarship, that allowed him to attend Trinity College at Cambridge University. He blew through his studies there (in a good way), and earned another degree by 1905.
At first, Eddington began researching thermionic emissions, but it didn't go very well. He had yet to find his niche.
I know Dear Reader. What the hell are thermionic emissions?
Well, let's see.
"The thermionic emission equation gives the current density of electrons as, {
D.29},
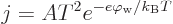
where
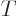is the absolute temperature and
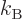is the Boltzmann constant. The constant
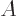is typically one quarter to one half of its theoretical value
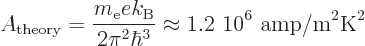(end quote)
OK. How about this:
"Thermionic emission is the emission of electrons from a heated metal (cathode). This principle was first used in the
Coolidge tube and then later in the modern day
x-ray tubes. Before the discovery of the principle,
gas tubes were used for
x-ray production."
Alright. When confronted with evolved theorems, you have to ask yourself: what is the end result?
Let's try this:
"Recognising the importance of ionisation in stellar interiors, he boldly assumed that because of the high ionisation of internal gases, the perfect-gas condition prevailed within the interiors of stars, except for 'white dwarfs'. This theory was later accepted.
He demonstrated that energy could be transported by radiation as well as by convection, and that the centres of stars must be at very high temperatures — in the millions of degrees."
The Dude abides....
Let's revisit that quote for a minute: "[h]e demonstrated that energy could be transported by radiation as well as by convection." I think we can understand one of the by-products from that work, right?
Another of Arthur's contributions is called the Eddington Model:
"The model was proposed by Eddington in the 1920s, when very little was known about physical properties of matter in stellar interiors. The model assumes, that pressure is provided by perfect, fully ionized gas and radiation, and that throughout a whole star the ratio of gas pressure to total pressure is constant: P = Pg + Pr, Pg = k µH ρT, Pr = a 3 T 4 , β ≡ Pg P = const. (ed.1) We may express temperature in two different ways: T = µH k Pg ρ = µH k βP ρ , T 4 = 3Pr a = 3 (1 − β) P a i.e., Pr P = 1 − β. (ed.2) These two expressions may be used to eliminate temperature, and find a relation between pressure and density: P = Kρ4/3 , K = " 3 a k µH 4 1 − β β 4 #1/3 , (ed.3) i.e. we have a polytropic relation with n = 3. K is constant throughout a star, because β was assumed to be constant. Of course, β as well as K may vary from one star to another. Other useful Eddington model expressions are: T = 3R µa 1/3 1 − β β 1/3 ρ 1/3 and 1 − β β = µSγ 4R , where Sγ = 4aT 3 3ρ is the specific radiation entropy. Entropy is an important quantity in stellar structure and evolution studies, even though one does not encounter it in texts as often as one should. We know that n = 3 polytrope is a special case: the total stellar mass is uniquely determined by the value of K : M = K 0.3639 G 1.5 = (0.3639 G) −1.5 " 3 a k µH 4 1 − β β 4 #1/2 . (ed.4) Another way of writing the above equation is 1 − β == 0.003 Mµ2 M⊙ 2 β 4 . The last equation gives another relation between stellar mass and β, which may be expressed as M M⊙ = 18.1 µ2 (1 − β) 1/2 β 2 . (ed.5) According to this equation gas pressure dominates, i.e. β → 1 when stellar mass is very small, and radiation pressure dominates, i.e. β → 0 when stellar mass is very large. The two contributions to pressure are equal, i.e. β = 0.5 when the stellar mass is M/M⊙ = 51/µ2 . For a solar mass star, i.e. for M/M⊙ = 1, and for the solar chemical composition, i.e. for µ ≈ 0.62, we have β ≈ 0.9995, i.e. radiation pressure may be neglected."
I know this stuff is fascinating (for some), but again one must ask: where does the science lead? To a greater understanding of the celestial realm, certainly, but what else is at the end of that yellow brick road? That's the real question, isn't it? Where did the various minds seeking out the significance of relativity inevitably take us? Well, here for starters:
Nagasaki, 1945.
I'm glad, though, that Eddington's work greatly aided in our understanding the structure of stars. I'm gonna concentrate on his comprehension of celestial matters, rather than energy release. Above all, though, I wanted to write a little bit about Arthur, because so many scientists and/or mathematicians are sometimes forgotten or overshadowed by the work of celebrities like Einstein (and Oppenheimer).
.gif)
.gif)
Comments
Post a Comment